时间序列分析中包含了许多复杂的数学公式，它们往往难以留存于记忆之中。为了更好地掌握这些内容，本文将整理并总结时间序列分析中的一些核心概念，如自协方差、自相关和平稳性等，并通过Python实现和图形化展示这些概念，使其更加直观易懂。希望通过这篇文章帮助大家更清楚地理解时间序列分析的基础框架和关键点。
时间序列与时间有关，随着时间的推移观察到的数据称为时间序列数据:例如，心率监测，每日最高温度等。虽然这些例子是有规律的间隔观察到的，但也有不规则间隔观察到的时间序列数据，如盘中股票交易、临床试验等。我们将使用定期观察跨度的时间序列数据，并且只有一个变量(单变量时间序列)。从数学上我们可以这样定义时间序列:
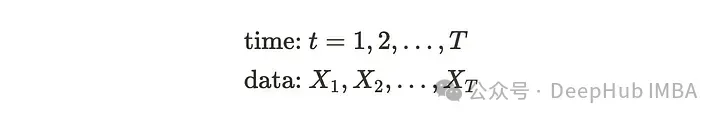
如果我们把X _l看作一个随机变量，可以定义一个依赖于观测时间t的均值和方差。
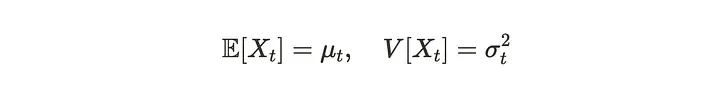
对于时间序列数据，可能想要比较过去和当前的数据。所以就引出了两个基本概念，自协方差和自相关
从技术上讲，自协方差和协方差是一样的。协方差有如下公式:
协方差计算两个变量X和y之间的关系。在计算样本协方差时，我们将每个观测值与平均值之间的差除以n-1，类似于样本方差。对于自协方差则计算前一个观测值与当前观测值之间的样本协方差。公式如下:
这里的h被称为滞后。滞后的X是前一个X值偏移了h位置。所以公式与协方差相同。
自相关也和相关一样，相关关系有如下公式。
相关性将协方差除以变量X和y的标准差，我们可以认为相关性类似于标准化协方差除以标准差。对于自相关，计算以前和当前观测值之间的相关性。h在公式中也表示滞后性。
当协方差和相关取较大的正值时，X和Y两个变量呈正相关关系。那么自协方差和自相关呢?我们来看看可视化。
对于第一个示例，从AR(1)流程生成数据(稍后我们将看到它)。它看起来像嘈杂的数据。
在这种情况下，自协方差和自相关图如下图所示。x轴表示滞后。
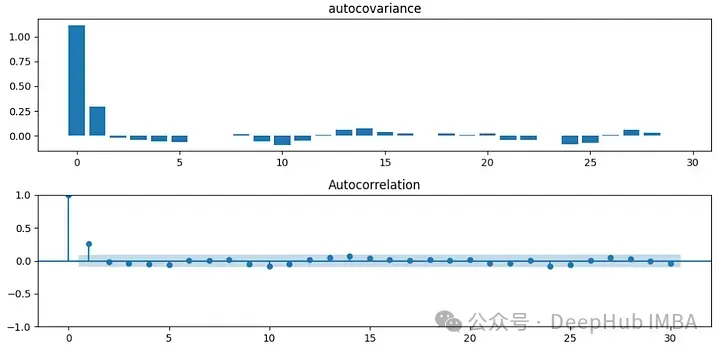
可以看到自协方差和自相关有相似的趋势。因此可以想象自相关可以被认为是标准化的自协方差。
对于下面的示例将使用真实世界的数据，例如AirPassengers[4]。airpassenger数据有明显的上升趋势。
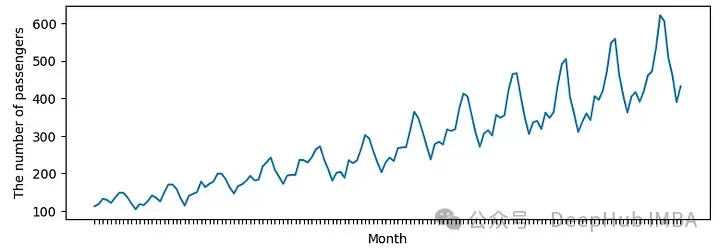
自协方差和自相关图如下图所示。x轴表示滞后。
自协方差和自相关也有类似的趋势。这个数据比第一个例子有更多的相关性和更大的滞后。
我们了解了两个关键概念，自协方差和自相关。接下来，我们讨论一个叫做平稳性的新概念。平稳时间序列意味着数据属性，如均值、方差和协方差，不依赖于观测时间。平稳性有两种类型:
该过程具有以下关系，称为弱平稳性，二阶平稳性或协方差平稳性。(有很多称呼它的方式。)
其中µ是常数，且
本文链接：//www.dmpip.com//www.dmpip.com/showinfo-26-100711-0.html统计学入门：时间序列分析基础知识详解 声明：本网页内容旨在传播知识，若有侵权等问题请及时与本网联系，我们将在第一时间删除处理。邮件：2376512515@qq.com 上一篇： 国内首个算力互联公共平台发布，可查询全国算力资源和调度服务 下一篇： C++20那些事之宇宙飞船运算符
Copyright © 2016-2023 天津谷骐科技有限公司 版权所有 sitemap.xml
违法及侵权请联系：2376512515@qq.com 津ICP备18001702号
津公网安备 12010102000574号
